Merkle Tree
Merkle Tree: Efficient Data Verification
Merkle trees enable efficient verification of large datasets without downloading everything. They’re like having a fingerprint for an entire library that proves any book belongs.
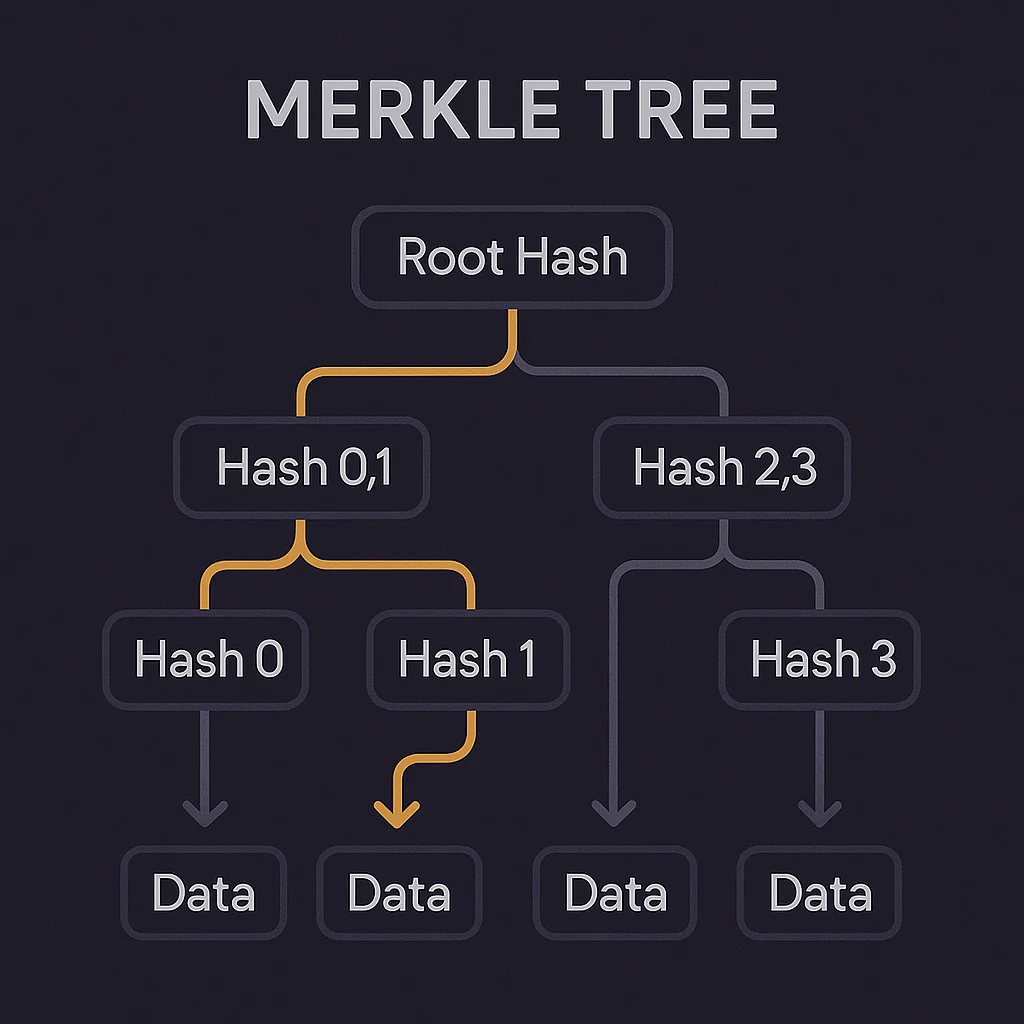
A Merkle tree is a binary tree structure where each leaf represents a data element and each branch contains cryptographic hashes of its children. The root hash summarizes the entire dataset, enabling quick verification of any element’s inclusion.
How Merkle Trees Work
Bottom-up hashing combines pairs of data elements into parent hashes, continuing until a single root hash represents the entire tree structure.
Inclusion proofs require only a small subset of hashes (the “Merkle path”) to prove any specific element exists in the tree without revealing other elements.
Tamper detection makes any change to underlying data immediately visible since it would change the root hash, alerting observers to modifications.
 ]
]
Real-World Examples
- Bitcoin blocks use Merkle trees to summarize all transactions in the block header
- IPFS storage employs Merkle trees for content addressing and verification
- Airdrop claims often use Merkle trees to efficiently verify eligibility without revealing all addresses
Why Beginners Should Care
Efficient verification allows light clients to verify specific transactions without downloading entire blockchains, enabling mobile and web wallets.
Privacy benefits from Merkle trees let systems prove inclusion without revealing the complete dataset to verifiers.
Scalability foundation for many Layer 2 solutions and blockchain optimizations that need to efficiently prove large amounts of data.
Related Terms: Hash Function, Light Client, Data Verification, Cryptographic Proof
